

Either we can put 5 and the bag will become full and the cost will be 14 or we can put 2, the bag will not be full and the cost will be 15. the cost of weight 2 as the second weight 5 cannot be accommodated. So, we will put 15 as we have a weight of 2 which does not violate the bag capacity and gives the highest price.Īfter this, when j=3 and 4, we will still have dp=15 i.e. the values are copied from the previous row. Maximum Sum of 3 Non-Overlapping SubarraysĢ nd Row: As discussed above, the value at dp when j<2 will remain 0 i.e. Maximum Sum Of M Non-overlapping Subarrays Maximum Sum Of Three Non-overlapping Subarrays Maximum Sum Of Two Non-overlapping Subarrays Maximum Difference Of Zeros And Ones In Binary String

Maximum Sum Subarray With At Least K Elements Minimum Cost To Make Two Strings Identical If you like it, please share your thoughts in the comment.Print All Longest Increasing SubsequencesĬount Of Distinct Palindromic Subsequences
0 1 knapsack code#
You can find the code on my GitHub repository. So, in this post, we learned about yet another problem that sounds tricky but actually pretty simple. The time and space complexity of this approach is O(n)(W). log ( "Maximum value: " + getMaximumValue ( W, n, weights, values ) ) Let this function be defined as -įunction getMaximumValue ( W, n, weights, values ) const weights = const values = const W = 50 const n = weights. We need to define a function that will give us the maximum value. Do you see the pattern? Yes, at each step the problem is reduced to a smaller problem. If we don’t select 20, then we will still have W = 50 and remaining list of items. At this point, we only have to solve the problem for W = 30. I put this in the Knapsack, now, what is the capacity left of the Knapsack? The answer is, 50(total weight W) - 20(weight of the selected item) = 30. For e.g., let me choose item with weight 20. Let us randomly select an item from the list of items. Your task is to maximize the combined value keeping total weight of items 50, this cannot be the solution.įrom above, we can easily deduce that items with weight 20 and 30 are the correct combination to choose.īut come on, do we really want to do this 😒? Don’t we have a better solution? In fact, we do! The answer is good old dynamic programming. You are given a fixed weight W (shopping cart’s capacity) and items with a certain weight w and value v.
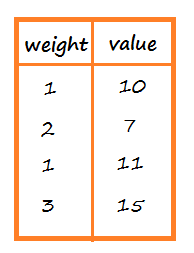
Does this ring a bell 🔔? Yes, this is exactly we are trying to accomplish in Knapsack problem.

What will you do? Of course, you will try to choose the values so that your selection will have the maximum values keeping in mind that your cart doesn’t get overfilled. Also, you cannot pick an item more than once. But there’s a catch… the only condition is that the items you choose cannot overfill the cart. You can choose as many items as you can 😍. Suppose your neighborhood store is giving an offer where they will give you a shopping cart and will ask you to go inside the store to fill the cart with any item (with a certain value) of your choice. What’s better than a real world example to understand something. But don’t worry, we can understand this together in simpler terms. Wait… what? 😕 confused? You’re supposed to be. Any item can either be selected or not selected (0 or 1). Our task is to choose the items whose combined weights is less than or equal to W with the maximum value. We will be given a bunch of items with certain weights w and values v along with maximum weight W a Knapsack can hold. Let’s first understand what is the ask in this problem? What do we need to find out? And it is another one of the most popular problem in computer science. The Knapsack Problem is a problem in combinatorial optimization which means one has to find optimal object from a set of finite objects.


 0 kommentar(er)
0 kommentar(er)
